שימו לב: על מנת להריץ את התאים ב-Live Code, יש לייבא תחילה את ספרית numpy ע”י הרצת השורת הבאה:

import numpy as np
import matplotlib.pyplot as plt
import imageio

פעולות בסיסיות על מערכי numpy ותמונות

ביחידה זו נכיר תכונות ופעולות שונות שניתן לבצע במערכי numpy, ונדגים אותם על המערכים “רגילים” כמו גם על מערכים המייצגים תמונות.

מימדי המטריצה

גישה למימדי מטריצה קיימת

נתחיל מהגדרת המטריצה הבאה:

b = np.array([[3, 4, 5], [6, 7, 8]])
print('b is \n' , b)

b is 
 [[3 4 5]
 [6 7 8]]

למדנו ביחידות הקודמות שlen תחזיר לנו את אורך האובייקט. מה לדעתם הערך שיוחזר מlen עבור המטריצה שלנו?

print(len(b))

2

כלומר, עבור מערכי numpy, len מחזירה את מספר השורות במטריצה.
במערך חד-מימדי len תחזיר את מספר האלמנטים במערך, בדומה לרשימה.

ואם נרצה לקבל את כל מימדי המטריצה שלנו? לצורך כך נשתמש בתכונה shape:

print(b.shape)

(2, 3)

שינוי מימדי מטריצות קיימות

ניתן גם לשחלף את המטריצה שלנו ע”י שימוש בתכונה T (כמו Transpose).
שימו לך שמימדי המטריצה המשוחלפת התהפכו!

print('b is \n',b)
print('b transposed is \n',b.T)
print('b transposed dimensions are: ',b.T.shape)

b is 
 [[3 4 5]
 [6 7 8]]
b transposed is 
 [[3 6]
 [4 7]
 [5 8]]
b transposed dimensions are:  (3, 2)

מלבד שחלוף, קיימת פונקציה בשם reshape, המאפשרת לשנות את מבנה המטריצה. מתודה זה תשים את האיברים של המטריצה המקורית, לפי סדר השורות, במטריצה חדשה בעלת מימדים שהועברו בקלט.

c = b.reshape((3,2))
print(c)

[[3 4]
 [5 6]
 [7 8]]

**שימו לב **

המימדים המועברים בקלט המתודה reshape חייבים לייצג מטריצה אשר תכיל את כל איברי המערך ממנו הופעלה המתודה. אחרת נקבל שגיאה.

לדוגמאות לעיל, פלט המתודה reshape אינו זהה למטריצה המשוחלפת, זאת מכיוון שבמטריצה המשוחלפת השורות הופכות לעמודות, וב-reshape סדר האיברים לפני שורות נשמר

כעת נדגים מה כיצד הפעולות שראינו למעלה מתבטאות במטריצות המייצגות תמונות:

על מנת לקבל את מספר השורות והעמודות בתמונה נוכל להשתמש בתכונה shape:

im_dog = imageio.v3.imread('files/dog.png')
print(im_dog) 

[[ 88  88  88 ...  61  60  60]
 [ 89  88  88 ...  61  60  60]
 [ 89  89  89 ...  61  61  61]
 ...
 [143 143 145 ... 103 102 102]
 [144 145 149 ... 103 102 102]
 [144 145 149 ... 103 102 102]]

print(im_dog.shape)

(302, 335)

ועל מנת להפוך את התמונה על צידה נוכל להשתמש בתכונה T

im_transposed = im_dog.T
plt.imshow(im_transposed,cmap='gray')

<matplotlib.image.AxesImage at 0x7f036f69c110>

גישה לערכים במטריצה

חילוץ ערך בודד ממטריצה

בדומה לרשימות, גם בnumpy ניתן לגשת לערכים ספציפיים בתמונה, כולל Slicing.

הייחודיות של Numpy היא שניתן לגשת לאיבר (או איברים) במטריצה (לדוגמא, mat) ע”י אינדקס השורות (x) והעמודות (y) יחדיו בתוך הסוגריים המרובעים בצורה הבאה: mat[x,y]

נדגים זאת בקוד הבא:

תחילה ניצור מטריצה 3X3 של סדרת המספרים בין 0 ל8:

a=np.arange(9).reshape((3,3))
print(a)

[[0 1 2]
 [3 4 5]
 [6 7 8]]

כעת נחלץ את האיבר האמצעי של המטריצה:

print(a[1, 1])

4

כלומר, חילצנו את האיבר שנמצא באינקס 1 של השורות (שורה שניה) ובאינדקס 1 של עמודות (עמודה שניה):

חילוץ תתי מטריצות

כדי להחזיר שורה שלמה, פשוט לא נעביר אינדקס עמודות. לדוגמא, כך נחזיר את כל השורה השניה:

print(a[1])

[3 4 5]

ומה עם נרצה להחזיר את כל העמודה השניה? חייבים לשים משהו לפני הפסיק…
במקרה זה, נשים פשוט נקודותיים : בדומה לslciing נקודותיים מחזירה את כל הטווח (כלומר, את כל השורות).

לדוגמא, כך נחזיר את העמודה השניה:

print(a[:,1])

[1 4 7]

באופן אנלוגי לרשימות, גם כאן ניתן לבצע השמות של איבורים למטריצה קיימת באמצעות פירוט אינדקסים הרלוונטיים:

a[1, 1] = 10
print(a)

[[ 0  1  2]
 [ 3 10  5]
 [ 6  7  8]]

ניתן גם להחזיר או לבצע הרשמה על תת-קבוצה של שורות/עמודות. לדוגמא:

a[0,0:2] = a[2,1:3]*10
print(a)

[[70 80  2]
 [ 3 10  5]
 [ 6  7  8]]

ניתן אף לפרט בדיוק אילו אינדקסים רוצים להחזיר ובאיזה סדר באמצעות רשימה (או Iterable מספרי אחר) בשורות את בעמודות. לדוגמא:

print(a[[2,1,2], 2])

[8 5 8]

תרגול: החזרת תתי-מטריצות באמצעות Slicing

תחילה נגדיר את המטריצה mat הבאה:

mat= np.array([[0, 1, 2,3,4,5],
            [10, 11, 12,13,14,15],
            [20, 21, 22,23,24,25],
            [30, 31, 32,33,34,35],
            [40, 41, 42,43,44,45],
            [50, 51, 52,53,54,55]])
print(mat)

[[ 0  1  2  3  4  5]
 [10 11 12 13 14 15]
 [20 21 22 23 24 25]
 [30 31 32 33 34 35]
 [40 41 42 43 44 45]
 [50 51 52 53 54 55]]

כעת, עבור כל אחת מארבעת הצבעים במטריצה להלן, כתוב שורה בודדת המבצעת Slicing על mat כדי לקבל את תת-מטריצה המסומנת ע”י אותו הצבע:

חיתוך שורות

# Write you code here

פתרון

print(mat[0,3:5])

חיתוך עמודות

# Write you code here

פתרון

print(mat[:,2])

תת מטריצה רציפה

# Write you code here

פתרון

print(mat[4:,4:])

תת-מטריצה עם קפיצות

# Write you code here

פתרון

print(mat[2::2,::2])

עריכת מטריצה קיימת

באופן אנלוגי לרשימות, גם כאן ניתן לערוך מטריצה קיימת באמצעות השמה.

ניצור תחילה מטריצה חדשה כפי שעשינו קודם:

a=np.arange(9).reshape((3,3))
print(a)

[[0 1 2]
 [3 4 5]
 [6 7 8]]

כעת נבצע השמה של איברים למטריצה קיימת באמצעות פירוט האינדקסים הרלוונטיים:

a[1, 1] = 10
print(a)

[[ 0  1  2]
 [ 3 10  5]
 [ 6  7  8]]

ניתן גם לבצע השמה על חלק מהשורות או העמודות. לדוגמא:

a[0,0:2] = a[2,1:3]*10
print(a)

[[70 80  2]
 [ 3 10  5]
 [ 6  7  8]]

מאחר שתמונות הן מטריצות מספרים בטווח 0-256, ניתן לערוך תמונות באמצעות שינוי ערכי המטריצה.

למטה נראה שתי דוגמאות לעריכת תמונה באמצעות Slicing.

נתחיל מקטע הקוד הבא:

new_fig = np.zeros((100,100))
new_fig[::2,::2] = 255

ודאו שהבנתם כיצד שתי השורות ההלו יוצרות את התמונה המופיעה למטה:

plt.imshow(new_fig, cmap=plt.cm.gray)

<matplotlib.image.AxesImage at 0x7f036f43ac50>

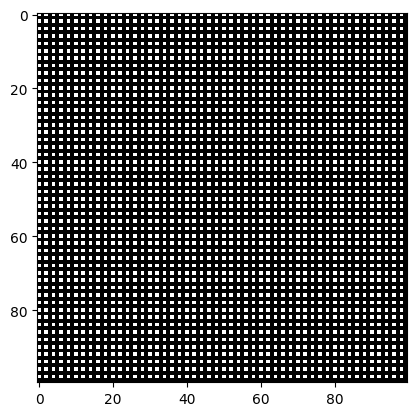
כעת, נניח שאנחנו רוצים להציג תמונה ברזולוציה נמוכה יותר, כלומר, לייצג תמונה עם פחות פיקסלים בזכרון (חשבו: מדוע שנרצה לעשות זאת?). בדוגמא הבאה, עבור ריבועים (לא חופפים) של 10X10 פיקסלים, נשאיר את הפיקסל השמאלי העליון:

im2=im_dog[::10,::10]

plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.imshow(im_dog, cmap=plt.cm.gray)
plt.subplot(1, 2, 2)
plt.imshow(im2, cmap=plt.cm.gray)

<matplotlib.image.AxesImage at 0x7f036c33cd50>

ערכים בוליאניים והשוואות במערכי numpy

השוואות במערכי numpy מתבצעות בדומה לאופרטורים מתמטיים.
אם משווים בין שני מערכים מאותם מימדים, הההשוואה נעשית איבר איבר.
אם משווים בין מערך לערך מסוים, כלל האיברים במערך יושוו לאותו הערך.
בשני המקרים, נקבל מערך בוליאני במימדי המערך (או המערכים) שבפעולת ההשוואה .

דוגמאות:

a = np.arange(6).reshape(2,3)
print("a: ", a)

b = np.arange(4,-2,-1).reshape(2,3)
print("b: ", b)

print(a<2)
print(a==b)

a:  [[0 1 2]
 [3 4 5]]
b:  [[ 4  3  2]
 [ 1  0 -1]]
[[ True  True False]
 [False False False]]
[[False False  True]
 [False False False]]

בהינתן מערך המכיל ערכים בוליאניים, ניתן להשתמש בany על מנת לבדוק האם לפחות אחד מהערכים במערך הוא True, כמו פעולת or בין כל איברי המערך.
באופן אנלוגי, ניתן גם להשתמש בall על מנת לבדוק האם כל הערכים במערך הוא True, כמו פעולת and בין כל איברי המערך.

comp1=a==b
print("### a==b ###")
print("any: ", comp1.any())
print("all: ",comp1.all())

print("### a<6 ###")
comp2=a<6
print("any: ",comp2.any())
print("all: ",comp2.all())

print("### a>6 ###")
comp3=a>6
print("any: ",comp3.any())
print("all: ",comp3.all())

### a==b ###
any:  True
all:  False
### a<6 ###
any:  True
all:  True
### a>6 ###
any:  False
all:  False

כפי שלמדנו ניתן להתייחס לערכים הבוליאניים False ו-True גם כמספרים 0 ו-1 בהתאמה.

לכן, ניתן להפעיל עליהם גם מתודות numpy.

בדוגמא למטה, אנו מפעילים את nonzero, המחזירה את כל האינדקסים של המערך בהם מופיע ערך שאינו 0, על מטריצה בוליאנית (כלומר, כל מקום בו מופיע True).

print("### a==b ###")
print(comp1.nonzero())

### a==b ###
(array([0]), array([2]))

דוגמא נוספת היא המתודה sum הסוכמת את כל איברי המטריצה

print("### a==b ###")
print(comp1.sum())

### a==b ###
1

חשבו

מדוע החזירו המתודות nonzero ו-sum את הערכים שהודפסו לעיל עבור a==b?

תרגול מסכם

בשאלות הבאות תתנסו במימוש הפונקציותany וall בעצמכם:

התחילו ממימוש הפונקציה array_any אשר מקבלת מטריצה בוליאנית, ומחזירה אם קיים בו איבר שהוא True. אין להשתמש במתודה any!

יש לממש את הפתרון בשורה אחת בלבד.

def array_any(array):
    # Write your code here
    pass

לחצו כאן כדי לצפות בפתרון

def array_any(array):
    # Write your code here
    return array.sum()>=1

כעת ממשו את הפונקציה array_all אשר מקבלת מערך בוליאני דו-מימדי, ומחזירה אם כל האיברים בו הם True. אין להשתמש במתודה all!

יש לממש את הפתרון בשורה אחת בלבד.

def array_all(array):
    # Write your code here
    pass

לחצו כאן כדי לצפות בפתרון

def array_all(array):
    # Write your code here
    return array.sum() == array.shape[0] * array.shape[1]